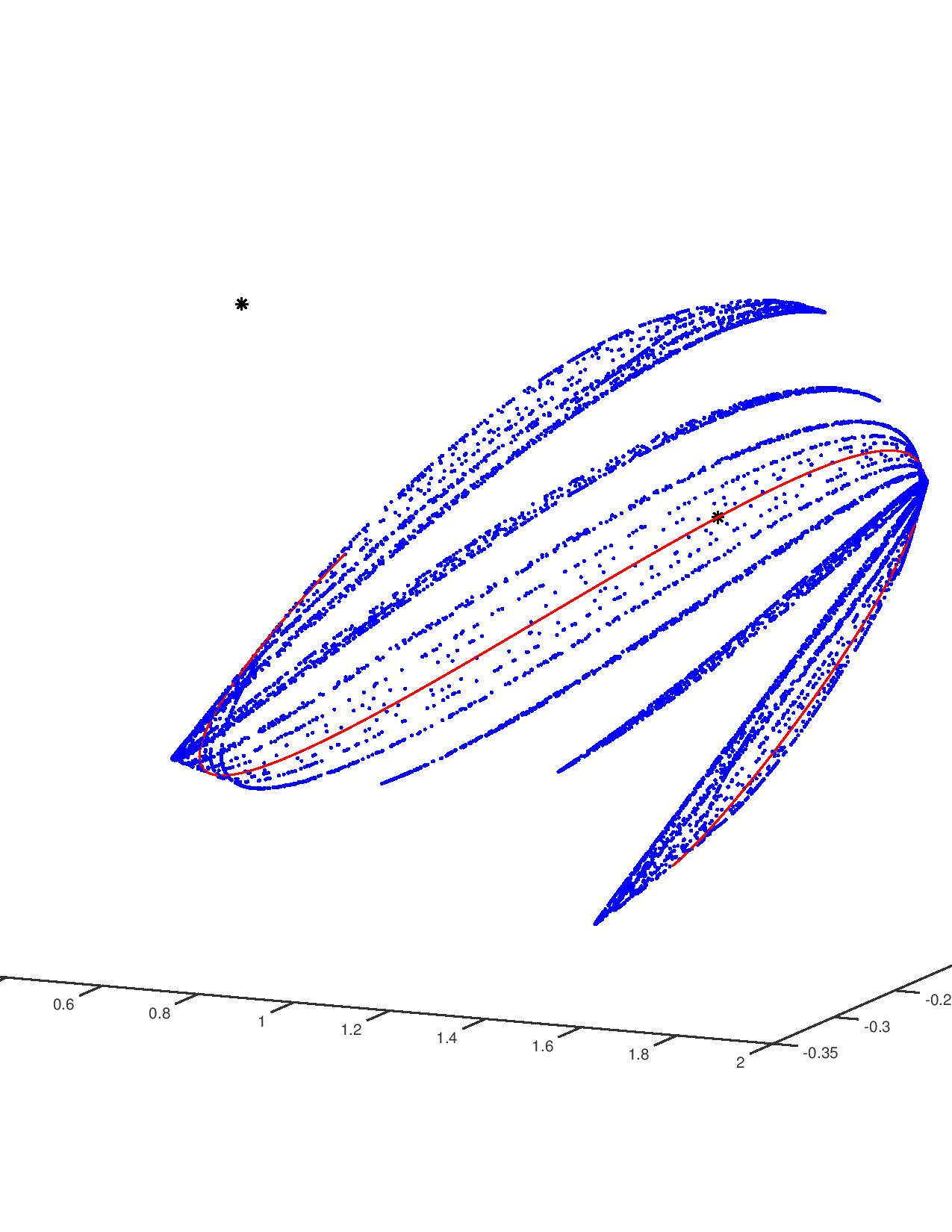
Abstract: We develop and implement a semi-numerical method for computing high order Tay- lor approximations of the unstable manifold at a hyperbolic fixed point of a compact infinite dimensional analytic map. Even though the method involves several layers of truncation our goal is to obtain a representation of the invariant manifold which is accurate in a large region about the fixed point. In order to insure the accuracy of our computations we develop a-posteriori error bounds for the approximations. Numerical implementation of the a-posteriori theory, combined with deliberate control of float- ing point round-off errors (or interval arithmetic), leads to mathematically rigorous computer assisted theorems describing precisely the truncation errors for the approxi- mation of the invariant manifold. The method is illstrated for the Kot-Schaffer model of population dynamics.
Author:
Jason D. Mireles James
Preprint:
Foundations of Computational Mathematics, Volume 17, pp. 1467-1523 (2017).
Computer Assisted Proof Codes:
(codes require the IntLab package)