Answer [1]: Nearer the Moon; actually, the position is about 10% of the Moon-Earth distance from the center of the Moon.
Answer [2]: By Newton's 3rd Law, the weight of the Earth in the gravitational field of the Earth is equal but opposite to the weight of the apple in the gravitational field of the Earth. So the answer is 1N.
Answer [3]: Objects weigh less at high altitudes because they are further from the center of the Earth. So to get the most mass for a given weight, you should buy at high altitude and sell at lower altitude where its weight would be more.
Answer [4]: The gravitational field at the surface of an object depends on its radius as well as its mass. So, if the radius of Jupiter was the same as the Earth and its mass was 300-Earth masses, then the gravitational force at its surface would be 300 times that on Earth. However, since its radius is somewhat greater than the Earth's radius, the gravitational force is correspondingly much reduced.
Answer [5]: Since the increase in the gravitational force at the surface is 3 times instead of 300 times, the radius of Jupiter must be 10 times that of the Earth. (Remember, the force is inversely proportional to the square of the radius.)
Answer [6]: You are "weightless" when there are no supporting forces and gravity is the only force acting on you. A skydiver is acted on by air resistance and a scuba diver experiences a buoyant force, i.e., an upthrust, and so they are not weightless. However, the astronaut is weightless.
Answer [7]: Umm ... very interesting question ... and answer! Our "Earthweight" is determined by the gravitational force of the Earth on us and the Sun does not affect our local weight. The reason is that we and the Earth are both falling towards the Sun as we orbit the Sun. So, just as a person in car that falls off a cliff is not "pressed" into the seat no matter how strong the Earth's gravitational force, our weight is not affected by the Sun's gravitational force.
Answer [8]: The answer is 4.9m/s2. At half-radius, it turns out that the mass of the outer shell, i.e., further out than half-radius, plays no role; the gravitational attraction from all parts of this shell cancels to zero. Only the mass of the Earth between the center and the half-radius point plays a role. The mass of a sphere of radius R/2 is 1/8 the mass of a sphere of radius R; why? ... because the volume depends on r3. The gravitational force depends not only on mass but inversely on the square of the distance from the center of the Earth. At R/2, the effect is a 4-fold increase. So, combining a 1/8 decrease with a 4-fold increase results in a change by a factor of 1/2.
Answer [9]: If the Earth had a uniform density then one's weight would decrease. An increase in weight then indicates that the density of the Earth increases towards the center. The increase in density more than overcomes the loss of gravitational effect by the outer shell.
Answer [10]: On a shrinking star your weight would increase because the gravitational attraction increases as you approach the center of mass of the star. If you tunnel into the star, however, the shell outside of you cancels an increasing portion of the gravitational force and so you weigh less.
Answer [11]: The diameter of the cable would have to be about 9600km, i.e., about 75% of the diameter of the Earth!
Using values of the masses of the Earth and Sun and the Earth-Sun distance from the book you will find that the gravitational attraction between the Earth and Sun is about 3.6 × 1022N. The required cross sectional area of the cable is then (3.6 × 1022)/(5 × 108) = 7.2 × 1013m2, which corresponds to a diameter of 9.6 × 106m. I bet you didn't think the attractive force was that large!
Answer [12]: The Earth rotates towards the east, so, by sending a satellite towards the east we can take advantage of the "extra" component of the velocity that the Earth's rotation provides. At the equator the tangential velocity of the Earth is nearly 0.5km/s with respect to the center of the Earth, but at higher latitudes the velocity decreases, and is zero at the poles. This extra velocity comes for free, i.e., it doesn't have to be provided by the rocket engines.
Answer [13]: Yes, there is no reason why a satellite could not orbit the Earth in a tunnel below the surface.
There are some interesting features, however. The orbital speed (given by v = √(gr)) would be less than at the surface, since both g, the acceleration of gravity and r would both be smaller. (g would be smaller because the mass of the Earth below the tunnel radius would be smaller than at the surface.) So, interestingly, a satellite in a circular orbit has its greatest speed at the Earth's surface (~8km/s), but the speed decreases with both decreasing and increasing distances! (With the latter, although r increases linearly, the rate of decrease of g is greater and so, overall, the speed decreases with altitude.)
Answer [14]: Actually, it can be done very simply!

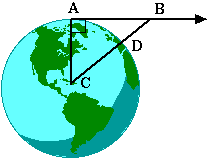
Think of a satellite fired tangentially from the point A, just above the Earth's surface. If there were no gravitational force, the satellite would follow the straight line path from A to B. However, there is a gravitational force and the satellite "falls" below the line AB (towards the center of the Earth, C). In order to remain in the near-Earth orbit the satellite would have to "fall" the distance BD. Now, we have:
But AC = DC = 6400km.
If we take AB to be the tangential distance the satellite would travel in 1 second, then BD would be the distance it would have to "fall" in 1 second, because of gravity, to remain in orbit. Now, all objects fall a distance ~4.9m in 1 second ... remember: (y - yo = (1/2)gt2) ... near the Earth's surface. Then
i.e., AB = 7920m.
But this is the tangential distance the satellite would travel in 1 second; so the tangential speed for a stable near-Earth orbit is 7920m/s; this translates to about 17,700mi/h!
Neat huh? ... and we've only used values of the Earth's radius and g.
Answer [15]: No, a wrench dropped by an astronaut on the space lab would not fall to the Earth. The reason is that when released, the wrench will have the same tangential speed as the space lab, which will be sufficient for it to continue in orbit around the Earth.
Although the wrench dropped from the jumbo jet will have the same tangential speed as the jet, i.e., 550mph, that speed is far less than the tangential speed required to maintain an object in a near-Earth orbit, which is ~8km/s (nearly 18,000mph). As a result, the wrench falls towards the Earth and eventually crashes.
Answer [16]: With respect to the Earth's surface, the capsule will have a (tangential) speed equal to zero. As a result, it will simply drop vertically towards the Earth and crash.
Answer [17]: The answer is 11.2km/s (25,000mph), i.e., the Earth's escape speed!
To understand why that is the case, remember that to determine the escape speed we used the work- kinetic energy theorem to equate the decrease in kinetic energy with the work done to move the object from the Earth' surface to a very distance point (infinity) against the Earth's gravitational force. If we reverse the process and start with an object at a very distant location, the work done by the Earth's gravitational force produces an increase in kinetic energy (from zero) that is equal to the work done; numerically this is the same as before so the "landing speed" - or rather, the "crashing speed" - is the same as the "launching speed".
Answer [18]: If you recall the work-energy theorem, the work required to launch will be the change in kinetic energy, which, for identical spacecraft, will depend on the escape speed. Since the escape speed of the Earth (~11.2km/s) is greater than that of the Moon (~2.4km/s), more fuel is required to have an Earth launch. In fact, it will require roughly (11.2/2.4) ~4.7 times as much fuel, neglecting air resistance and the change in mass as the fuel is used.
The escape velocity of Mars is ~5km/s and so it would require more fuel to escape Mars than it would the Moon.
Answer [19]: Since the rocket has an initial speed that is twice the escape speed (i.e., ~22.4km/s), it has kinetic energy that is four times greater than that required to escape. Therefore, once it has escaped, its kinetic energy is three times the escape energy, so its speed is √3 (= 1.732) times the escape speed (i.e., ~19.4km/s).
Answer [20]: There are a number of situations where the gravitational force decreases as the masses approach. One example is shown below ... a small mass (m) approaching a uniform, metal ring (of mass M) along its axis!
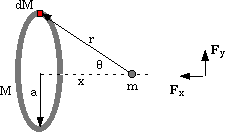
Consider the force on mass m on the axis of the ring due to the element of mass dM. The magnitude of the force is:
along the r direction. The components of dF are dFx and dFy. Now, if we sum the contributions from all mass elements around the ring - noting that |r| is constant - and providing the mass is uniformly distributed, we see that the resultant force perpendicular to the x-direction is zero, i.e., the resultant force is directed only along x. Then,
So, this is the attractive force beteen the two masses. Note:
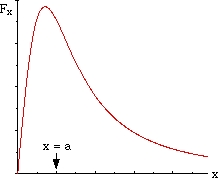
which shows clearly that the force decreases as we approach the center of the ring!
Other examples include approaching a square, rectangular or elliptical frame, along an axis perpendicular to the plane and passing through the center, traveling along the axis of a hollow tube, etc.