Authors:
Jaime Burgos-Garcia, J.P. Lessard and J.D. Mireles James

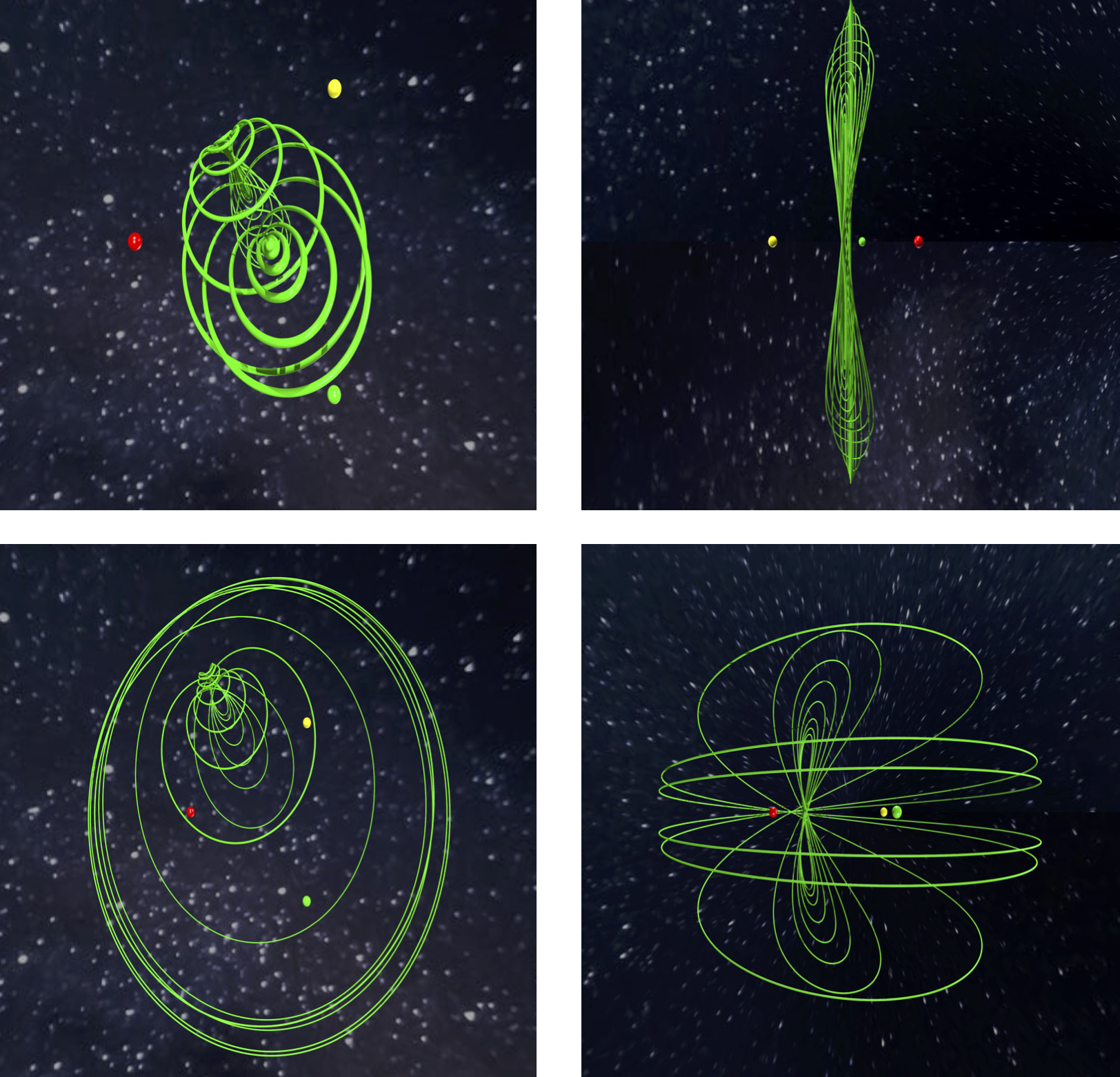
Abstract: We use validated numerical methods to prove the existence of spatial pe- riodic orbits in the equilateral restricted four body problem. We study each of the vertical Lyapunov families (up to symmetry) in the triple Copenhagen problem, as well as some halo and axial families bifurcating from planar Lyapunov families. We consider the system with both equal and nonequal masses. Our method is constructive and non-perturbative, being based on a-posteriori analysis of a certain nonlinear operator equation in the neighborhood of a suitable approximate solution. The approximation is via piecewise Chebyshev series with coefficients in a Banach space of rapidly decaying sequences. As byproduct of the proof we obtain useful quantitative information about the location and regularity of the solution.