Authors:
J.L. Gonzalez and J.D. Mireles James

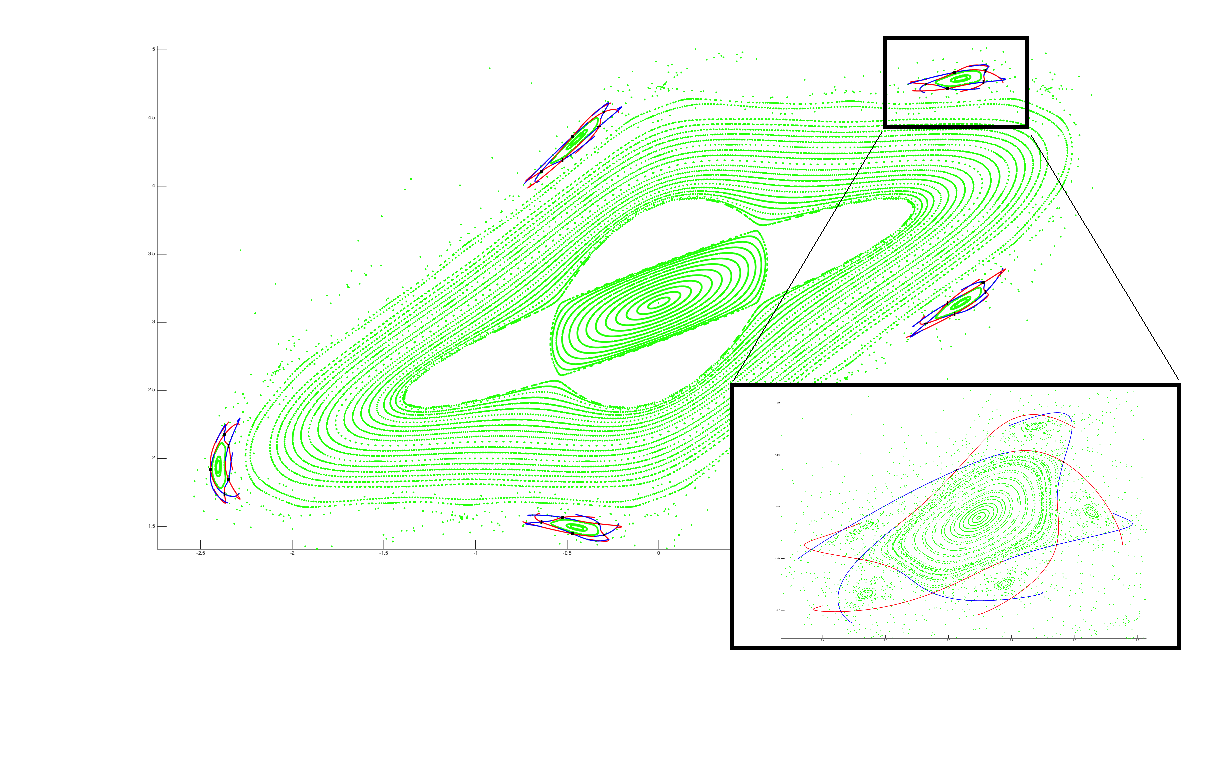
Abstract: We consider the problem of computing stable/unstable manifolds attached to periodic orbits of maps, and develop seminumerical methods for polynomial approximation of the manifolds to any desired order. Our approach avoids function compositions by exploiting an idea inspired by multiple shooting schemes for periodic orbits. We consider a system of conjugacy equations which characterize chart maps for the local stable/unstable manifold segments attached to the points of the periodic orbit. We develop a formal series solution for the system of conjugacy equations, and show that the coefficients of the series are determined by recursively solving certain linear systems of equations. We derive the recursive equations for some example problems in dimension two and three, and for examples with both polynomial and transcendental nonlinearities. Finally we present some numerical results which illustrate the utility of the method and highlight some technical numerical issues such as controlling the decay rate of the coefficients and managing truncation errors via a-posteriori indicators.