Authors: Jan Bouwe van den Berg
Jason D. Mireles-James
Jean-Philippe Lessard
Konstantin Mischaikow

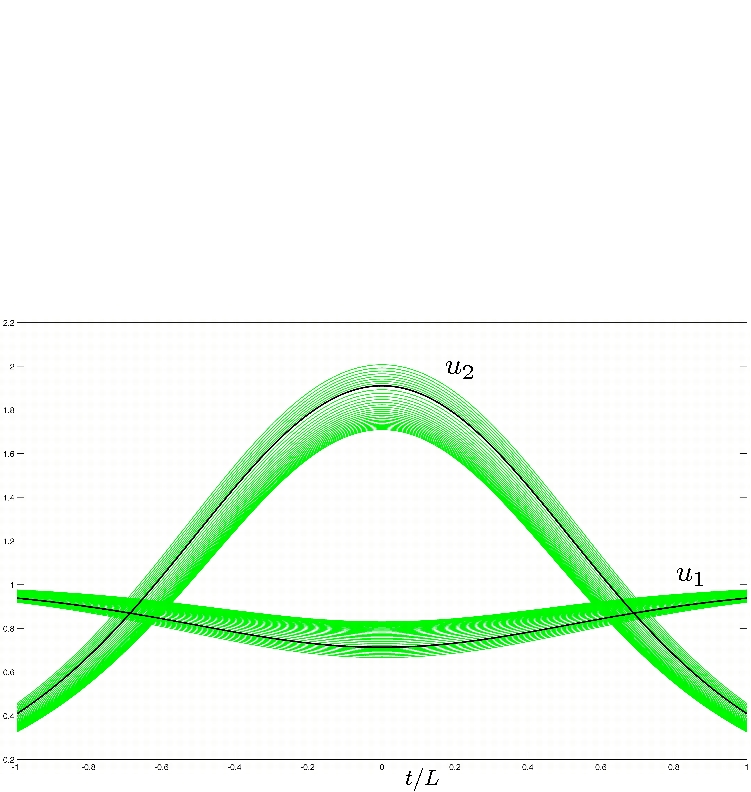
Abstract: In this paper we propose a rigorous numerical technique for the computation of symmetric connecting orbits for ordinary dierential equations. The idea is to solve a projected boundary value problem (BVP) in a function space via a fied point argument. The formulation of the projected BVP involves a high-order parameterization of the invariant manifolds at the steady states. Using this parameterization, one can obtain explicit exponential asymptotic bounds for the coefficients of the expansion of the manifolds. Combining these bounds with piecewise linear approximations, one can construct a contraction in a function space whose unique fixed point corresponds to the wanted connecting orbit. We have implemented the method to demonstrate its effectiveness, and we have used it to prove the existence of a family of even homoclinic orbits for the Gray-Scott system.