Research / Operator Theory
Isoperimetric Sandwiches in Operator Theory:
The shift operator on the Hardy space or Bergman space of the disk is not a normal operator.
One way to measure its "abnormality" is to take the operator norm of its self-commutator.
(The self-commutator vanishes for normal operators.)
This can be calculated exactly for the disk, but can be difficult for multiplication operators on other domains.
Putnam's inequality gives a (sharp estimate) that implies an upper bound in this setting.
D. Khavinson proved a lower bound for the norm of the self-commutator of Toeplitz operators acting on the Smirnov space of a domain.
Combined with Putnam's inequality (giving an upper bound) this provides the following sandwich:
\begin{equation}
\frac{ 4 \text{Area}^2 \left( G \right)}{ \text{Perim}^2(G) } \leq ||[T_{z}^*,T_{z}] || \leq \frac{\text{Area}(G)}{\pi}.
\end{equation}
As an appealing consequence this recovers the classical isoperimetric inequality (with sharp constants) relating area and perimeter of the underlying domain:
\begin{equation}
4 \pi \text{Area} \left( G \right) \leq \text{Perim}^2(G).
\end{equation}
Timothy Ferguson, Steve Bell, and I sought a lower estimate
for the operator norm of the self-commutator of
multiplication operators in a separate setting:
the Bergman Space (preprint).
We proved a lower bound in terms of the so-called "torsional rigidity",
a domain constant from elasticity theory.
When combined with Putnam's inequality
we recovered the Saint-Venant isoperimetric inequality for torsional rigidity,
but with non-sharp constants.
Based on sharpness of the constant in our lower bound,
we suspected that the deficiency in recovering the precise Saint-Venant inequality
was due to Putnam's inequality not being sharp in this setting.
We conjectured that even though Putnam's inequality is sharp in general
it could be improved by a factor of two
in the restricted setting of multiplication operators acting on Bergman space.
J-F. Olsen and M. C. Reguera proved our conjecture.
Their improved version of Putnam's inequality combined with our lower bound
together give a novel proof of the Saint-Venant inequality and provide another "isoperimetric sandwich" in this case connecting
Operator Theory with an isoperimetric inequality from Mathematical Physics:
$$ \frac{\rho}{\text{Area}(G)} \leq ||[T_{z}^*,T_{z}] || \leq \frac{\text{Area}(G)}{2 \pi},$$
for the self-commutator of the multiplication by z on the Bergman space of the domain G.
In particular, this implies the Saint-Venant inequality for the torsional rigidity:
$$ \rho \leq \frac{\text{Area}^2(G)}{2 \pi}.$$
Background on the torsional rigidity:
Given a beam with uniform cross section,
the torsional rigidity measures the beam's resistance to twisting.
It is the integral of the so-called torsion function,
the solution u of a variational problem whose Euler-Lagrange condition is
a Poisson equation with constant source and zero Dirichlet boundary values:
$$
\begin{cases}
\Delta u=-2 & \mathrm{in}\;G\\
u|_{\partial G}=0\\
\end{cases}.
$$
The torsion function also has an interpretation in terms of Brownian motion:
at each point in the domain the value of the torsion function
is the expected life-time of Brownian motion
starting from that point (and killed when it reaches the boundary).
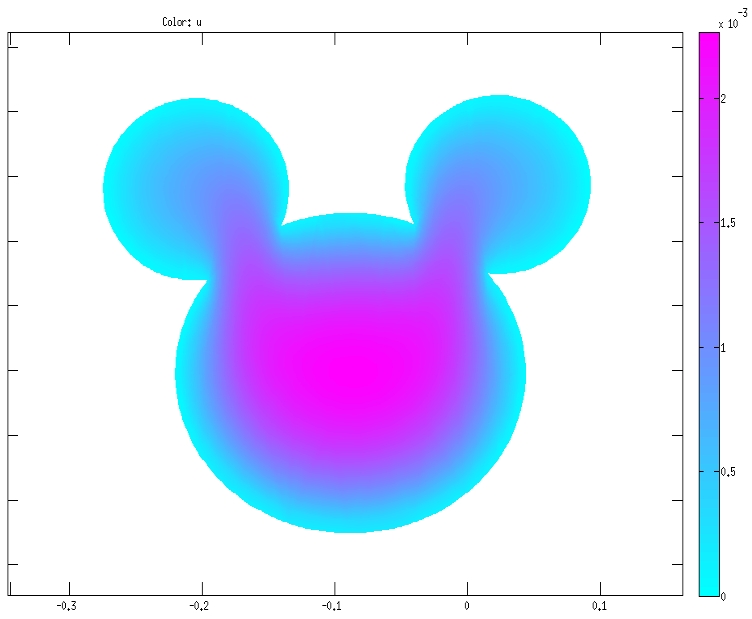
The torsion function of a domain shaded according to height (created using Matlab). The torsion constant is the integral over the domain of this function.
Saint-Venant's inequality states that among domains with fixed area, the torsional rigidity is maximized for the disk. Saint-Venant's inequality was conjectured by Saint-Venant in 1856. Polya was the first to give a proof in 1948.
The search for isoperimetric sandwiches: Are there other isoperimetric sandwiches waiting to be discovered? Proving one isoperimetric inequality using operator theory might be a fluke, but recasting two of them as operator norm sandwiches suggests that the same can be done for the other isoperimetric inequalities, such as fundamental frequency or capacity (see Polya and Szego's book "Isoperimetric Inequalities in Mathematical Physics"). What operator and what function space should be considered in order to recast, say, the Faber-Krahn inequality (for the fundamental frequency of a domain)?