Research / Univalent Harmonic Mappings
The mapping problem for polygons: The Rado-Kneser-Choquet Theorem implies that any convex polygon can be mapped from the unit disk by the Poisson integral of a step function, and this gives a univalent (one-to-one) harmonic map. What if the polygon is not convex, is it possible to choose a step function whose Poisson integral is a univalent harmonic map?
This is the mapping problem posed by T. Sheil-Small (1989). Note that the Schwarz-Christoffel map to a polygon is harmonic, but this problem asks for the map to be the Poisson integral of a step function, a special type of harmonic map that is related to Jenkins-Serrin minimal surfaces, of which Sherk's first surface is a simple example. For Sherk's first surface, the associated harmonic mapping sends four equal arcs to the vertices of a square. (With an appropriate choice of height function, this parameterizes the minimal surface.)
D. Bshouty, A. Weitsman, and I recently gave a complete solution to the mapping problem. Contrary to Sheil-Small's conjecture, we showed that any polygon bounding a Jordan domain can be mapped univalently by the Poisson integral of a step function (preprint).
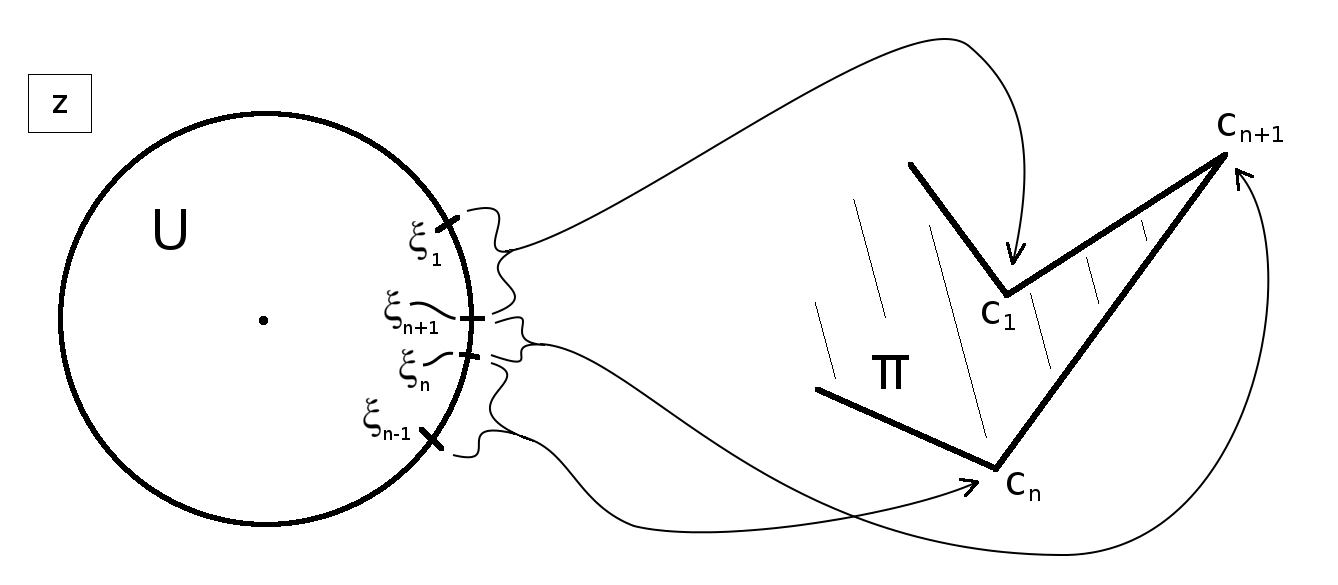
Our proof used an unexpected ingredient from computational geometry: the triangulation algorithm known as "ear clipping". The above image illistrates an inductive step in which the step function acquires a new interval which is sent to an "ear". The length of this interval must be chosen sufficiently small in order to preserve univalence (see the preprint for details).
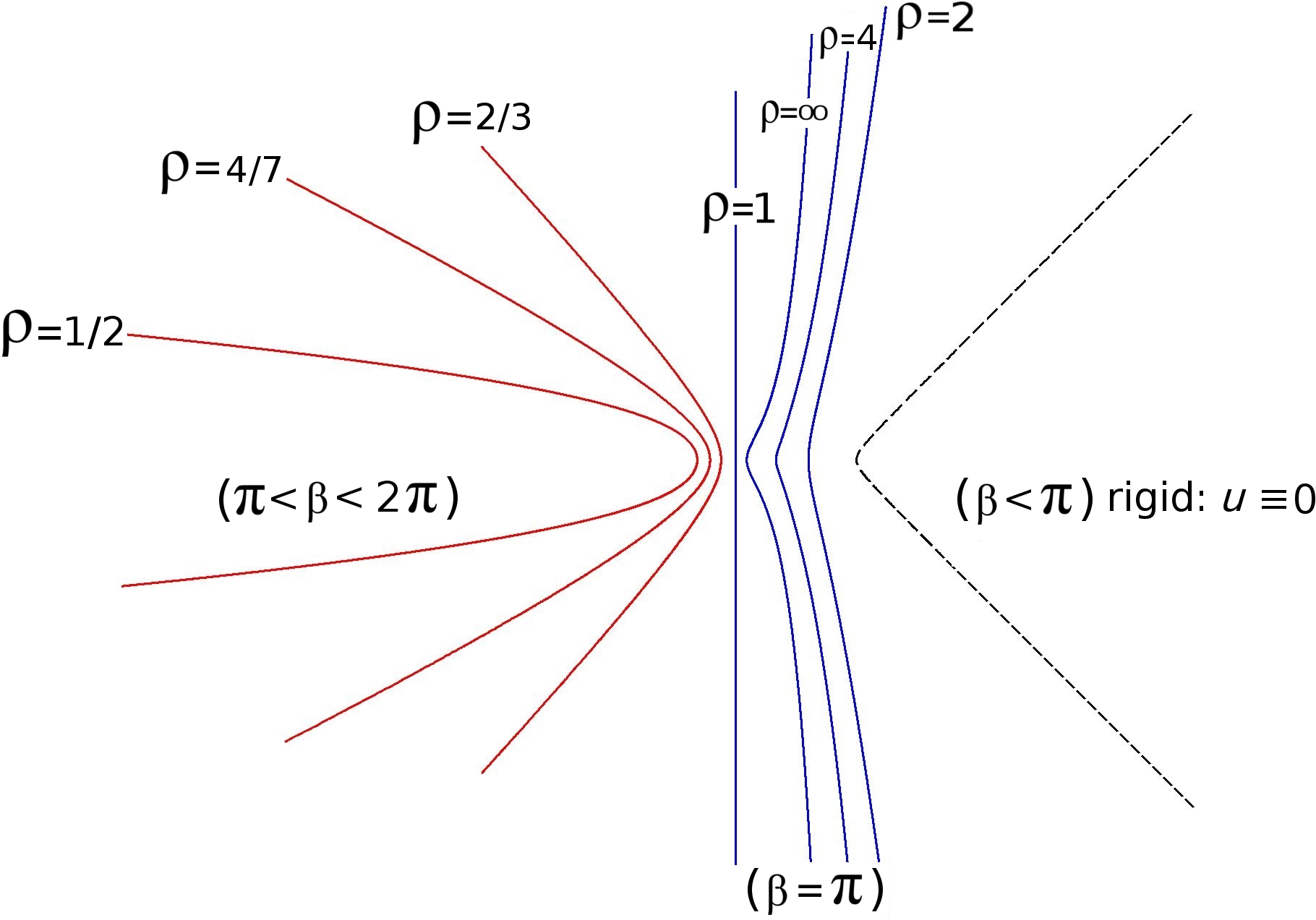
Minimal surfaces: An important classical application of univalent harmonic mappings is in parameterization of minimal surfaces. Allen Weitsman and I investigated the growth of minimal surfaces that are graphs over unbounded domains. We used techniques from planar harmonic mappings together with an associated height function. There is an interesting phase transition in the growth constraints for minimal graphs over domains (i) contained in a halfplane compared to (ii) containing a halfplane.
The image below shows the boundary of various domains (the domain is to the right of the curve) labelled with the order of growth of the height function for a minimal graph over that domain (and vanishing on the boundary). The phase transition is that the height functions associated to the red curves have at most linear growth (and the growth respects asymptotic angle, much like the Phragmen-Lindelof principle for harmonic functions), whereas the blue curves allow growth from linear to exponential (and all have the same asymptotic angle as the halfplane, thus exhibiting a sudden violent deviation from the behavior of linear elliptic equations).